论文信息

论文标题：MixMatch: A Holistic Approach to Semi-Supervised Learning 论文作者：David Berthelot, Nicholas Carlini, Ian Goodfellow, Nicolas Papernot, Avital Oliver, Colin Raffel 论文来源：NeurIPS 2019 论文地址： download   论文代码： download 引用次数：1898 。

1 Introduction

　　半监督学习[6]（SSL）试图通过允许模型利用未标记数据，减轻对标记数据的需求。最近的半监督学习方法在未标记的数据上增加一个损失项，鼓励模型推广到不可见的数据。该损失项大致可分：  。

• • 熵最小化（entropy minimization）[18,28]——鼓励模型对未标记数据产生高质信度的预测；
  • 一致性正则化（consistency regularization）——鼓励模型在输入受到扰动时产生相同的输出分布；
  • 通用正则化（generic regularization）——鼓励模型很好地泛化，避免过拟合；

2 Related Work

2.1 Consistency Regularization

　　监督学习中一种常见的正则化技术是数据增强，它被假定为使类语义不受影响的输入转换。例如，在图像分类中，通常会对输入图像进行变形或添加噪声，这在不改变其标签的情况下改变图像的像素内容。即：通过生成一个接近的、无限新的、修改过的数据流来人为地扩大训练集的大小.

　　一致性正则化将数据增强用于半监督学习，基于利用一个分类器应该对一个未标记的例子输出相同的类分布的想法。正式地说，一致性正则化强制执行一个未标记的样本 $x$ 应与 $\text{Augment(x)}$ 分类相同.

　　在最简单的情况下，对于未标记的样本 $x$，先前工作[25,40]添加如下损失项:

　　　　$\| \mathrm{p}_{\text {model }}(y \mid \operatorname{Augment}(x) ; \theta)-\mathrm{p}_{\text {model }}(y \mid \text { Augment }(x) ; \theta) \|_{2}^{2}\quad\quad(1)$ 。

　　注意，$\text{Augment(x)}$ 是一个随机变换，所以 $\text{Eq.1}$ 中的两项 $\text{Augment(x)}$ 是不完全相同的.

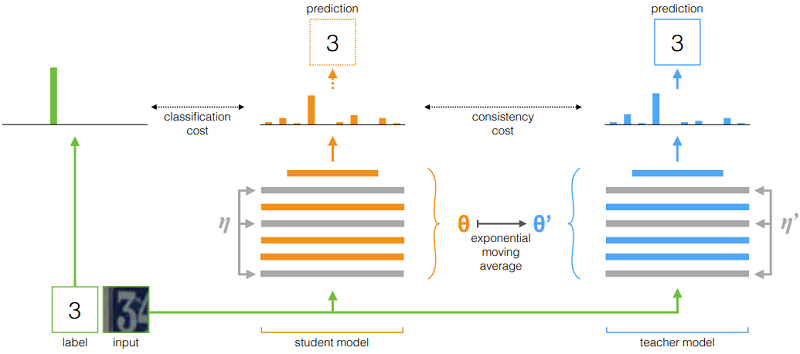
　　类似的操作 [44](基于模型参数扰动):

　　　　$\begin{array}{l} J(\theta)=\mathbb{E}_{x, \eta^{\prime}, \eta}\left[\left\|f\left(x, \theta^{\prime}, \eta^{\prime}\right)-f(x, \theta, \eta)\right\|^{2}\right]\\\theta_{t}^{\prime}=\alpha \theta_{t-1}^{\prime}+(1-\alpha) \theta_{t}\end{array}$ 。

　　图示:

2.2 Entropy Minimization

　　许多半监督学习方法中，一个基本假设是：分类器的决策边界不应该通过边缘数据分布的高密度区域。实现的一种方法是要求分类器对未标记的数据输出低熵预测，[18]中其损失项使未标记数据 $x$ 的 $\operatorname{p}_{\text {model}}(y \mid x ; \theta)$ 的熵最小化。$\text{MixMatch}$ 通过对未标记数据的分布使用 $\text{sharpening}$ 函数，隐式地实现了熵的最小化.

3 MixMatch 

　　给定一批具有 $\text{one-hot}$ 标签的样本集 $\mathcal{X}$ 和一个同等大小的未标记的样本集 $U$，$\text{MixMatch}$ 生成一批经过处理的增强标记样本 $\mathcal{X}^{\prime}$ 和一批带“猜测”标签的增强未标记样本 $\mathcal{U}^{\prime}$，然后使用 $\mathcal{U}^{\prime}$ 和 $\mathcal{X}^{\prime}$ 计算损失项:

　　　　$\begin{array}{l}\mathcal{X}^{\prime}, \mathcal{U}^{\prime} & =&\operatorname{MixMatch}(\mathcal{X}, \mathcal{U}, T, K, \alpha) \quad \quad \quad\quad\quad(2)\\\mathcal{L}_{\mathcal{X}} & =&\frac{1}{\left|\mathcal{X}^{\prime}\right|} \sum\limits_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}\left(p, \text { p }_{\text {model }}(y \mid x ; \theta)\right) \quad \quad\quad(3)\\\mathcal{L}_{\mathcal{U}} & =&\frac{1}{L\left|\mathcal{U}^{\prime}\right|} \sum\limits _{u, q \in \mathcal{U}^{\prime}}\|q-\operatorname{p}_{\text{model}}(y \mid u ; \theta)\|_{2}^{2} \quad \quad(4) \\\mathcal{L} & =&\mathcal{L}_{\mathcal{X}}+\lambda_{\mathcal{U}} \mathcal{L}_{\mathcal{U}}  \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(5)\end{array}$ 。

　　其中，$\text{H(p, q)}$ 代表着交叉熵损失.

3.1 Data Augmentation

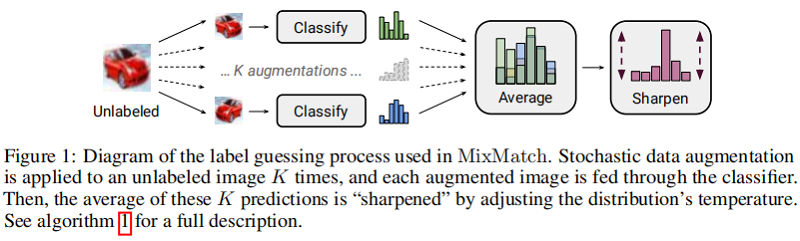
　　如许多 SSL 方法中的那样，对标记和未标记数据使用数据增强。对于一批带标记数据 $\mathcal{X}$ 中的每个 $x_{b}$ 生成一个数据增强样本 $\hat{x}_{b}=\operatorname{Augment}\left(x_{b}\right)$；对未带标记的数据集 $\mathcal{U}$ 中的样本 $u_{b}$，生成 $K$ 个数据增强样本 $\hat{u}_{b, k}=  \operatorname{Augment}  \left(u_{b}\right)$，$k \in(1, \ldots, K)$，下文为每个 $u_{b}$ 生成一个“猜测标签” $q_{b}$.

3.2 Label Guessing

　　对于 $\mathcal{U}$ 中的每个未标记的样本，$\text{MixMatch}$ 使用模型预测为该样本生成一个“猜测标签”，通过计算模型对 $u_b$ 的预测类分布的平均值:

　　　　$\bar{q}_{b}=\frac{1}{K} \sum\limits _{k=1}^{K} \operatorname{p}_{\text{model}}\left(y \mid \hat{u}_{b, k} ; \theta\right)\quad\quad(6)$ 。

　　接着使用 锐化函数（$\text{Sharpen}$） 来调整这个分类分布:

　　　　$\operatorname{Sharpen}(p, T)_{i}:=p_{i}^{\frac{1}{T}} / \sum\limits _{j=1}^{L} p_{j}^{\frac{1}{T}}\quad\quad(7)$ 。

　　其中，$p$ 是输入的类分布，此处 $p= \bar{q}_{b}$；$T$ 是超参数，当 $T \rightarrow 0$ 时，$\text{Sharpen(p,T)}$ 的输出接近 $\text{one-hot}$ 形式； 。

　　通过改小节内容为无标签样本 $u_{b}$ 产生预测分布，使用较小的 $T$ 会鼓励模型产生较低熵的预测.

3.3 MixUp

　　对于一个 Batch 中的样本（包括无标签数据和带标签数据），对于任意两个样本 $\left(x_{1}, p_{1}\right)$,$\left(x_{2}, p_{2}\right) $ 计算 $\left(x^{\prime}, p^{\prime}\right)$ :

　　　　$\begin{aligned}\lambda & \sim \operatorname{Beta}(\alpha, \alpha)\quad \quad \quad \quad\quad(8)\\\lambda^{\prime} & =\max (\lambda, 1-\lambda)\quad \quad \quad\quad(9)\\x^{\prime} & =\lambda^{\prime} x_{1}+\left(1-\lambda^{\prime}\right) x_{2}  \quad\quad(10)\\p^{\prime} & =\lambda^{\prime} p_{1}+\left(1-\lambda^{\prime}\right) p_{2}  \quad\quad(11)\end{aligned}$ 。

　　其中，$\alpha$ 是一个超参数.

　　鉴于已标记和未标记的样本在同一批中，需要保留该$\text{Batch}$ 的顺序，以适当地计算单个损失分量。通过 $\text{Eq.9}$ 确保 $x^{\prime}$ 更接近 $x_1$ 而不是 $x_2$。为了应用 $\text{MixUp}$，首先收集所有带有标签的增强标记示例和所有带有猜测标签的未标记示例:

　　　　$\begin{array}{l}\hat{\mathcal{X}}=\left(\left(\hat{x}_{b}, p_{b}\right) ; b \in(1, \ldots, B)\right)  \quad\quad(12)   \\\hat{\mathcal{U}}=\left(\left(\hat{u}_{b, k}, q_{b}\right) ; b \in(1, \ldots, B), k \in(1, \ldots, K)\right) \quad\quad(13)  \end{array}$ 。

　　完整算法如下:

4 Experiment

  。

最后此篇关于迁移学习（MixMatch）《MixMatch:AHolisticApproachtoSemi-SupervisedLearning》的文章就讲到这里了,如果你想了解更多关于迁移学习（MixMatch）《MixMatch:AHolisticApproachtoSemi-SupervisedLearning》的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。