- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
在前面文章中提到 空间直角坐标系相互转换 ,测绘坐标转换时,一般涉及到的情况是:两个直角坐标系的小角度转换。这个就是我们经常在测绘数据处理中,WGS-84坐标系、54北京坐标系、80西安坐标系、国家2000坐标系之间的转换.
所谓小角度转换,指直角坐标系 \(XOY\) 和直角坐标系 \(X'O'Y'\) 之间,对应轴的旋转角度很小, 满足泰勒级数展开后的线性模型 .
常见的三维坐标转换模型有 [1] :
但,当两个坐标系对应轴的旋转角度大道一定程度时,则无法使用低阶的泰勒级数展开,且迭代的计算量、精度、速度无法取得平衡 [2] 。存在以下缺点:
罗德里格矩阵 是摄影测量中的常见方法,在该方法中,不需要进行三角函数的计算和迭代运算。计算过程简单明了,易于编程实现。不仅适用于小角度的坐标转换,也适用于大角度的空间坐标转换.
本文将介绍罗德里格矩阵的基本原理和C#实现,并用实例证明解算的有效性.
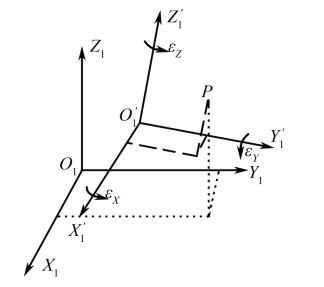
两个空间直角坐标系分别为 \(XOY\) 和 \(X'O'Y'\) ,坐标系原点不一致,存在三个平移参数 \(\Delta X\) 、 \(\Delta Y\) 、 \(\Delta Z\) 。它们间的坐标轴也相互不平行,存在三个旋转参数 \(\epsilon x\) 、 \(\epsilon y\) 、 \(\epsilon z\) 。同一点A在两个坐标系中的坐标分别为 \((X,Y,Z)\) 和 \((X',Y',Z')\) .
显然,这两个坐标系通过坐标轴的平移和旋转变换可取得,坐标间的转换关系如下
其中, \(\lambda\) 是比例因子, \(R\left(\varepsilon_Y\right) R\left(\varepsilon_X\right) R\left(\varepsilon_Z\right)\) 分别是绕Y轴,X轴,Z轴的旋转矩阵。 注意,旋转的顺序不同, \(R\) 的表达形式不同 .
习惯上称 \(R\) 为旋转矩阵, \([\Delta X,\Delta Y,\Delta Z]^T\) 为平移矩阵。只要求出 \(\Delta X\) 、 \(\Delta Y\) 、 \(\Delta Z\) , \(\varepsilon_X\) 、 \(\varepsilon_Y\) 、 \(\varepsilon_Z\) ,这7个转换参数,或者直接求出旋转矩阵和平移矩阵,就可以实现两个坐标系间的转换.
为计算方便,对所用到的坐标进行重心化处理。将两个坐标系的公共点的坐标均化算为以重心为原点的重心化坐标。分别记为 \((\bar{X}, \bar{Y}, \bar{Z})\) 和 \(\left(\bar{X}^{\prime}, \bar{Y}^{\prime}, \bar{Z}^{\prime}\right)\) 两个坐标系的重心的坐标分别为 \((X_g, Y_g, Z_g)\) 和 \((X'_g, Y'_g, Z'_g)\) .
因此,可以将式(1)变为:
因而,转换参数可分两步来求解。先用式(2)求出旋转参数和比例因子,再用式(,3)求出平移参数.
对式(2)两边取 2-范数 ,由于 \(\lambda > 0\) ,旋转矩阵为正交阵的特性,可得
对于n个公共点,可得 \(\lambda\) 的最小均方估计
得到比例因子的最小均方估计后,可将旋转矩阵 \(R\) 表示为
其中, \(I\) 为单位矩阵, \(S\) 为反对称矩阵。将式(5)带入式(3),可得:
矩阵运算使用 MathNet.Numerics 库,初始化字段 MatrixBuilder<double> mb = Matrix<double>.Build 和 VectorBuilder<double> vb = Vector<double>.Build 。
Vector<double> BarycentricCoord(Matrix<double> coordinate)
{
Vector<double> barycentric = vb.Dense(3, 1);
int lenCoord = coordinate.ColumnCount;
if (lenCoord > 2)
barycentric = coordinate.RowSums();
barycentric /= lenCoord;
return barycentric;
}
取2-范数使用 点乘 函数 PointwisePower(2.0) :
double ScaleFactor(Matrix<double> sourceCoord, Matrix<double> targetCoord)
{
double k = 0;
double s1 = 0;
double s2 = 0;
Vector<double> sourceColL2Norm = sourceCoord.PointwisePower(2.0).ColumnSums();
Vector<double> targetColL2Norm = targetCoord.PointwisePower(2.0).ColumnSums();
int lenSourceCoord = sourceCoord.ColumnCount;
int lenTargetCoord = targetCoord.ColumnCount;
//只有在目标矩阵和源矩阵大小一致时,才能计算
if (lenSourceCoord == lenTargetCoord)
{
s1 = sourceColL2Norm.PointwiseSqrt().PointwiseMultiply(targetColL2Norm.PointwiseSqrt()).Sum();
s2 = sourceColL2Norm.Sum();
}
k = s1 / s2;
return k;
}
这里的罗德里格参数就是式(6)中的 \([a, b, c]^T\) .
Vector<double> RoderickParas(double scalceFactor, Matrix<double> sourceCoord, Matrix<double> targetCoord)
{
Vector<double> roderick = vb.Dense(new double[] { 0, 0, 0 });
int lenData = sourceCoord.ColumnCount;
//常系数矩阵
var lConstant = vb.Dense(new double[3 * lenData]);
//系数矩阵
var coefficient = mb.DenseOfArray(new double[3 * lenData, 3]);
//构造相应矩阵
for (int i = 0; i < lenData; i++)
{
lConstant[3 * i] = targetCoord[0, i] - scalceFactor * sourceCoord[0, i];
lConstant[3 * i + 1] = targetCoord[1, i] - scalceFactor * sourceCoord[1, i];
lConstant[3 * i + 2] = targetCoord[2, i] - scalceFactor * sourceCoord[2, i];
coefficient[3 * i, 0] = 0;
coefficient[3 * i, 1] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]);
coefficient[3 * i, 2] = -(targetCoord[1, i] + scalceFactor * sourceCoord[1, i]);
coefficient[3 * i + 1, 0] = -(targetCoord[2, i] + scalceFactor * sourceCoord[2, i]);
coefficient[3 * i + 1, 1] = 0;
coefficient[3 * i + 1, 2] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i];
coefficient[3 * i + 2, 0] = targetCoord[1, i] + scalceFactor * sourceCoord[1, i];
coefficient[3 * i + 2, 1] = targetCoord[0, i] + scalceFactor * sourceCoord[0, i];
coefficient[3 * i + 2, 2] = 0;
}
roderick = coefficient.TransposeThisAndMultiply(coefficient).Inverse() * coefficient.Transpose() * lConstant;
return roderick;
}
此处,就是式(5)的实现.
/// <summary>
/// 解析罗德里格矩阵为旋转矩阵和平移矩阵
/// </summary>
/// <param name="scaleFactor">比例因子</param>
/// <param name="roderick">罗德里格矩阵</param>
/// <param name="coreSourceCoord">原坐标系坐标</param>
/// <param name="coreTargetCoord">目标坐标系坐标</param>
/// <returns></returns>
(Matrix<double>, Vector<double>) RotationMatrix(double scaleFactor, Vector<double> roderick, Vector<double> coreSourceCoord, Vector<double> coreTargetCoord)
{
Matrix<double> rotation = mb.DenseOfArray(new double[,]
{
{0,0,0 },
{0,0,0 },
{0,0,0 }
});
//反对称矩阵
Matrix<double> antisymmetric = mb.DenseOfArray(new double[,]
{
{ 0, -roderick[2], -roderick[1] },
{roderick[2], 0, -roderick[0] },
{roderick[1], roderick[0], 0 }
});
// 创建单位矩阵
// 然后与式(5)的 S 执行 + 和 - 操作
rotation = (DenseMatrix.CreateIdentity(3) - antisymmetric).Inverse() * (DenseMatrix.CreateIdentity(3) + antisymmetric);
translation = coreTargetCoord - scaleFactor * rotation * coreSourceCoord;
return (rotation, translation);
}
// 1. 字段值准备
MatrixBuilder<double> mb = Matrix<double>.Build;
VectorBuilder<double> vb = Vector<double>.Build;
// 2. 写入源坐标系的坐标。注意这里的x,y,z输入顺序
Matrix<double> source = mb.DenseOfArray(new double[,]
{
{-17.968, -12.829, 11.058 },
{-0.019 , 7.117, 11.001 },
{0.019 , -7.117, 10.981 }
}).Transpose();
// 3. 写入目标坐标系的坐标
Matrix<double> target = mb.DenseOfArray(new double[,]
{
{ 3392088.646,504140.985,17.958 },
{ 3392089.517,504167.820,17.775 },
{ 3392098.729,504156.945,17.751 }
}).Transpose();
// 4. 重心化
var coreSource = BarycentricCoord(source);
var coreTarget = BarycentricCoord(target);
var sourceCoords = source - mb.DenseOfColumnVectors(coreSource, coreSource, coreSource);
var targetCoords = target - mb.DenseOfColumnVectors(coreTarget, coreTarget, coreTarget);
// 5. 求比例因子
double k = ScaleFactor(sourceCoords, targetCoords);
// 6. 解算咯德里格参数
var roderick = RoderickParas(k, sourceCoords, targetCoords);
// 7. 旋转
(Matrix<double> ro, Vector<double> tran) = RotationMatrix(k, roderick, coreSource, coreTarget);
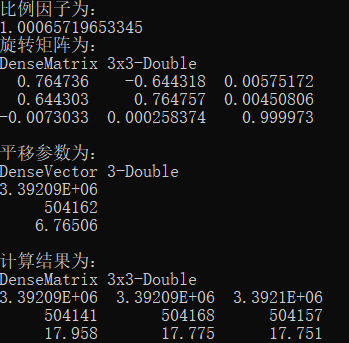
Console.WriteLine("比例因子为:");
Console.WriteLine(k);
Console.WriteLine("旋转矩阵为:");
Console.WriteLine(ro.ToString());
Console.WriteLine("平移参数为:");
Console.WriteLine(tran.ToString());
Console.WriteLine("计算结果为:");
Console.WriteLine(source2.ToString());
基于罗德里格矩阵的转换方法,在求解两个坐标系间的转换参数,特别是旋转角较大时,实现简单、快速.
朱华统,杨元喜,吕志平.GPS坐标系统的变换[M].北京:测绘出版社,1994. ↩︎ 。
詹银虎,郑勇,骆亚波,等.无需初值及迭代的天文导航新算法0﹒测绘科学技术学报,2015,32(5):445-449. ↩︎ 。
最后此篇关于大角度非迭代的空间坐标旋转C#实现的文章就讲到这里了,如果你想了解更多关于大角度非迭代的空间坐标旋转C#实现的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
#include using namespace std; class C{ private: int value; public: C(){ value = 0;
这个问题已经有答案了: What is the difference between char a[] = ?string?; and char *p = ?string?;? (8 个回答) 已关闭
关闭。此题需要details or clarity 。目前不接受答案。 想要改进这个问题吗?通过 editing this post 添加详细信息并澄清问题. 已关闭 7 年前。 此帖子已于 8 个月
除了调试之外,是否有任何针对 c、c++ 或 c# 的测试工具,其工作原理类似于将独立函数复制粘贴到某个文本框,然后在其他文本框中输入参数? 最佳答案 也许您会考虑单元测试。我推荐你谷歌测试和谷歌模拟
我想在第二台显示器中移动一个窗口 (HWND)。问题是我尝试了很多方法,例如将分辨率加倍或输入负值,但它永远无法将窗口放在我的第二台显示器上。 关于如何在 C/C++/c# 中执行此操作的任何线索 最
我正在寻找 C/C++/C## 中不同类型 DES 的现有实现。我的运行平台是Windows XP/Vista/7。 我正在尝试编写一个 C# 程序,它将使用 DES 算法进行加密和解密。我需要一些实
很难说出这里要问什么。这个问题模棱两可、含糊不清、不完整、过于宽泛或夸夸其谈,无法以目前的形式得到合理的回答。如需帮助澄清此问题以便重新打开,visit the help center . 关闭 1
有没有办法强制将另一个 窗口置于顶部? 不是应用程序的窗口,而是另一个已经在系统上运行的窗口。 (Windows, C/C++/C#) 最佳答案 SetWindowPos(that_window_ha
假设您可以在 C/C++ 或 Csharp 之间做出选择,并且您打算在 Windows 和 Linux 服务器上运行同一服务器的多个实例,那么构建套接字服务器应用程序的最明智选择是什么? 最佳答案 如
你们能告诉我它们之间的区别吗? 顺便问一下,有什么叫C++库或C库的吗? 最佳答案 C++ 标准库 和 C 标准库 是 C++ 和 C 标准定义的库,提供给 C++ 和 C 程序使用。那是那些词的共同
下面的测试代码,我将输出信息放在注释中。我使用的是 gcc 4.8.5 和 Centos 7.2。 #include #include class C { public:
很难说出这里问的是什么。这个问题是含糊的、模糊的、不完整的、过于宽泛的或修辞性的,无法以目前的形式得到合理的回答。如需帮助澄清此问题以便重新打开它,visit the help center 。 已关
我的客户将使用名为 annoucement 的结构/类与客户通信。我想我会用 C++ 编写服务器。会有很多不同的类继承annoucement。我的问题是通过网络将这些类发送给客户端 我想也许我应该使用
我在 C# 中有以下函数: public Matrix ConcatDescriptors(IList> descriptors) { int cols = descriptors[0].Co
我有一个项目要编写一个函数来对某些数据执行某些操作。我可以用 C/C++ 编写代码,但我不想与雇主共享该函数的代码。相反,我只想让他有权在他自己的代码中调用该函数。是否可以?我想到了这两种方法 - 在
我使用的是编写糟糕的第 3 方 (C/C++) Api。我从托管代码(C++/CLI)中使用它。有时会出现“访问冲突错误”。这使整个应用程序崩溃。我知道我无法处理这些错误[如果指针访问非法内存位置等,
关闭。这个问题不符合Stack Overflow guidelines .它目前不接受答案。 我们不允许提问寻求书籍、工具、软件库等的推荐。您可以编辑问题,以便用事实和引用来回答。 关闭 7 年前。
已关闭。此问题不符合Stack Overflow guidelines 。目前不接受答案。 要求我们推荐或查找工具、库或最喜欢的场外资源的问题对于 Stack Overflow 来说是偏离主题的,因为
我有一些 C 代码,将使用 P/Invoke 从 C# 调用。我正在尝试为这个 C 函数定义一个 C# 等效项。 SomeData* DoSomething(); struct SomeData {
这个问题已经有答案了: Why are these constructs using pre and post-increment undefined behavior? (14 个回答) 已关闭 6

我是一名优秀的程序员,十分优秀!