- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
本文已收录到 AndroidFamily ,技术和职场问题,请关注公众号 [彭旭锐] 提问.
大家好,我是小彭.
在前面的文章里 ,我们聊到了计算机的冯·诺依曼架构的 3 个基本原则。其中第 1 个原则是计算机中所有信息都是采用二进制格式的编码。也就是说,在计算机中程序的数据和指令,以及用户输入的所有数据,计算机都需要把它们转换为二进制的格式,才能进行识别和运算.
然而,我们日常生活接触到的大部分数字却是十进制编码,例如手机号码、工牌号、学号。那为什么计算机要使用二进制数制?二进制数据如何进行运算,以及计算机做了哪些优化来如何提高运算的效率?今天我们就围绕这些问题展开.
小彭的 Android 交流群 02 群已经建立啦,扫描文末二维码进入~ 。
思维导图:
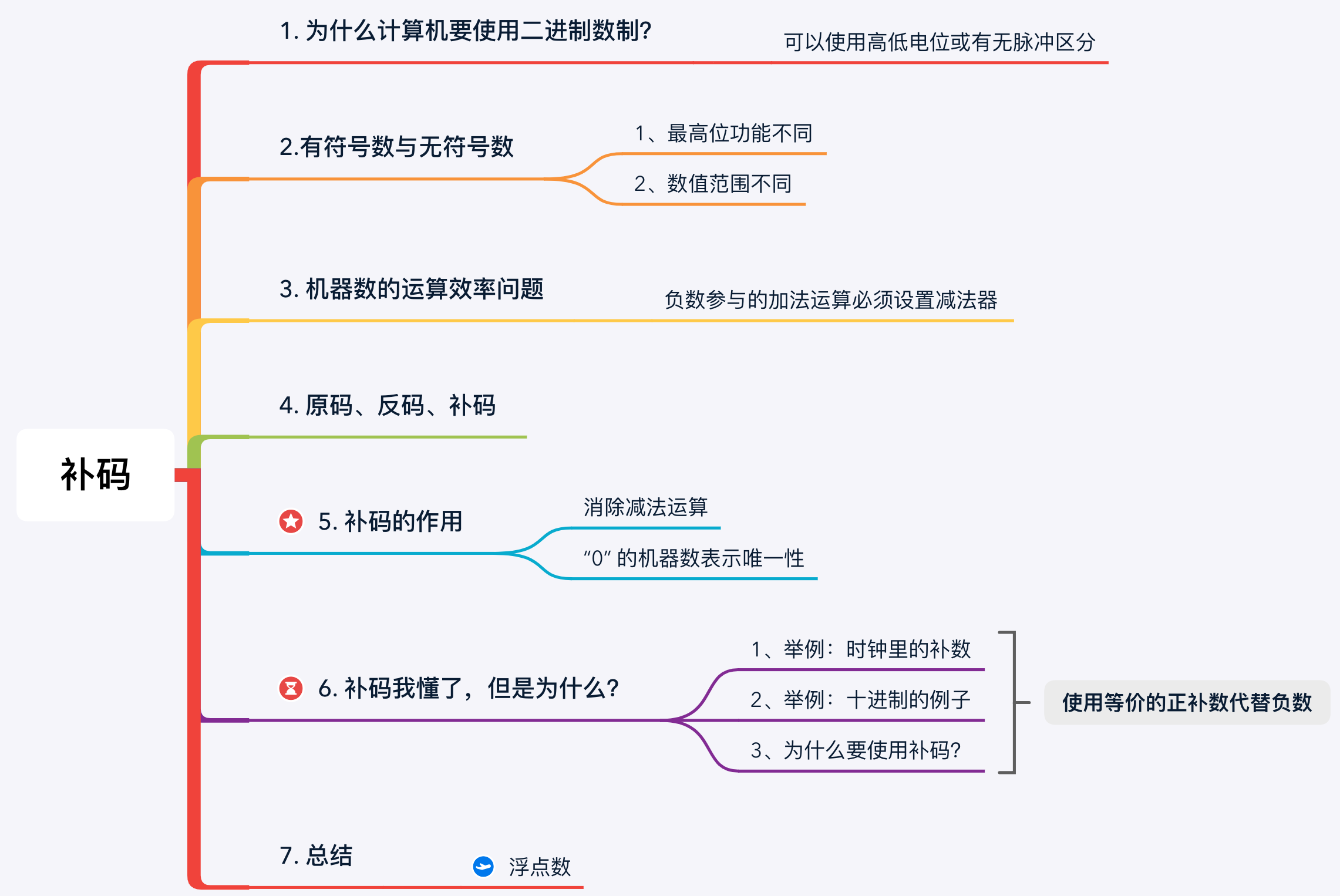
所谓数制其实就是一种 “计数的进位方式”.
常见的数制有十进制、二进制、八进制和十六进制:
十进制是我们日常生活中最熟悉的进位方式,它一共有 0、1、2、3、4、5、6、7、8 和 9 十个符号。在计数的过程中,当某一位满 10 时,就需要向它临近的高位进一,即逢十进一; 。
二进制是程序员更熟悉的进位方式,也是随着计算机的诞生而发展起来的,它只有 0 和 1 两个符号。在计数的过程中,当某一位满 2 时,就需要向它临近的高位进一,即逢二进一; 。
八进制和十六进制同理.
那么,为什么计算机要使用二进制数制,而不是人类更熟悉的十进制呢?其原因在于二进制只有两种状态,制造只有 2 个稳定状态的电子元器件可以使用高低电位或有无脉冲区分,而相比于具备多个状态的电子元器件会更加稳定可靠.
在计算机中会区分有符号数和无符号数,无符号数不需要考虑符号,可以将数字编码中的每一位都用来存放数值。有符号数需要考虑正负性,然而计算机是无法识别符号的 “正+” 或 “负-” 标志的,那怎么办呢?
好在我们发现 “正 / 负” 是两种截然不同的状态,正好可以映射到计算机能够理解的 “0 / 1” 上。因此,我们可以直接 “将符号数字化”,将 “正+” 数字化为 “0”,将 “负-” 数字化为 “1”,并将数字化后的符号和数值共同组成数字编码.
另外,为了计算方便,我们额外再规定将 “符号位” 放在数字编码的 “最高位”。例如, +1110 和 -1110 用 8 位二进制表示就是:
从中我们也可以看出无符号数和有符号数的区别:
1、最高位功能不同: 无符号数的编码中的每一位都可以用来存放数值信息,而有符号数需要在编码的最高位留出一位符号位; 。
2、数值范围不同: 相同位数下有符号数和无符号数表示的数值范围不同。以 16 位数为例,无符号数可以表示 0~65536,而有符号数可以表示 -32768~32768.
提示: 无符号数和有符号数表示的数值范围大小是一样大的,n 位二进制最多只能表示 $2^n$ 个信息量,这是无法被突破的.
在计算机中,我们会把带 “正 / 负” 符号的数称为真值(True Value),而把符号化后的数称为机器数(Computer Number).
机器数才是数字在计算机中的二进制表示。 例如在前面的数字中, +1110 是真值,而 0000, 1110 是机器数。新的问题来了:将符号数字化后的机器数,在运算的过程中符号位是否与数值参与运算,又应该如何运算呢?
我们先举几个加法运算的例子:
0000, 1110 + 0000, 0001 = 0000, 1111 // 14 + 1 = 15 正确
^ ^ ^
符号位 符号位 符号位
1000, 1110 + 1000, 0001 = 0000, 1111 // (-14) + (-1) = 15 错误
^ ^ ^
符号位 符号位 符号位(最高位的 1 溢出)
0000, 1110 + 1000, 0001 = 1001, 1111 // 14 + (-1) = -15 错误
^ ^ ^
符号位 符号位 符号位
可以看到,在对机器数进行 “按位加法” 运算时,只有两个正数的加法运算的结果是正确的,而包含负数的加法运算的结果却是错误的,会出现 -14 - 1 = 15 和 14 - 1 = -15 这种错误结果.
所以,带负数的加法运算就不能使用常规的按位加法运算了,需要做特殊处理:
两个正数相加:
两个负数相加:
正负数相加:
哇🤩?好好的加法运算给整成减法运算? 运算器的电路设计不仅要多设置一个减法器,而且运算步骤还特别复杂。那么,有没有不需要设置减法器,而且步骤简单的方案呢?
为了解决有符号机器数运算效率问题,计算机科学家们提出多种机器数的表示法:
| 机器数 | 正数 | 负数 |
|---|---|---|
| 原码 | 符号位表示符号 数值位表示真值的绝对值 |
符号位表示数字的符号 数值位表示真值的绝对值 |
| 反码 | 无(或者认为是原码本身) | 符号位为 1 数值位是对原码数值位的 “按位取反” |
| 补码 | 无(或者认为是原码本身) | 在负数反码的基础上 + 1 |
1、原码: 原码是最简单的机器数,例如前文提到从 +1110 和 -1110 转换得到的 0000, 1110 和 1000, 1110 就是原码表示法,所以原码在进行数字运算时会存在前文提到的效率问题; 。
2、反码: 反码一般认为是原码和补码转换的中间过渡; 。
3、补码: 补码才是解决机器数的运算效率的关键, 在计算机中所有 “整型类型” 的负数都会使用补码表示法; 。
很多教材和网上的资料会认为正数的原码、反码和补码是相同的,这么说倒也不影响什么。 但结合补码的设计原理,小彭的观点是正数是没有反码和补码的,负数使用补码是为了找到一个 “等价” 的正补数代替负数参与计算,将加减法运算统一为两个正数加法运算,而正数自然是不需要替换的,所以也就没有补码的形式.
提示: 为了便于你理解,小彭后文会继续用 “正数的补码是原码本身” 这个观点阐述.
理解补码表示法后,似乎还是不清楚补码有什么用❓ 。
我们重新计算上一节的加法运算试试:
| 举例 | 真值 | 原码 | 反码 | 补码 |
|---|---|---|---|---|
| +14 | +1110 | 0000, 1110 | 0000, 1110 | 0000, 1110 |
| +13 | +1101 | 0000, 1101 | 0000, 1101 | 0000, 1101 |
| -14 | +1110 | 1000, 1110 | 1111, 0001 | 1111, 0010 |
| -15 | -1110 | 1000, 1111 | 1111, 0000 | 1111, 0001 |
| +1 | +0001 | 0000, 0001 | 0000, 0001 | 0000, 0001 |
| -1 | -0001 | 1000, 0001 | 1111, 1110 | 1111, 1111 |
// 补码表示法
0000, 1110 + 0000, 0001 = 0000, 1111 // 14 + 1 = 15 正确
^ ^ ^
符号位 符号位 符号位
// 补码表示法
1111, 0010 + 1111, 1111 = 1111, 0001 // (-14) + (-1) = -15 正确
^ ^ ^
符号位 符号位 符号位(最高位的 1 溢出)
// 补码表示法
0000, 1110 + 1111, 1111 = 0000, 1101 // 14 + (-1) = 13 正确
^ ^ ^
符号位 符号位 符号位(最高位的 1 溢出)
可以看到,使用补码表示法后,有符号机器数加法运算就只是纯粹的加法运算,不会因为符号的正负性而采用不同的计算方法,也不需要减法运算。因此电路设计中只需要设置加法器和补数器,就可以完成有符号数的加法和减法运算,能够简化电路设计.
除了消除减法运算外,补码表示法还实现了 “0” 的机器数的唯一性:
在原码表示法中,“+0” 和 “-0” 都是合法的,而在补码表示法中 “0” 只有唯一的机器数表示,即 0000, 0000 。换言之补码能够比原码多表示一个最小的负数 1000, 0000 .
最后提供按照不同表示法解释二进制机器数后得到的真值对比:
| 二进制数 | 无符号真值 | 原码真值 | 反码真值 | 补码真值 |
|---|---|---|---|---|
| 0000, 0000 | 0 | +0 | +0 | +0 |
| 0000, 0001 | 1 | +1 | +1 | +1 |
| … | … | … | … | … |
| 1000, 0000 | 128 | -0(负零,无意义) | -127 | -128(多表示一个数) |
| 1000, 0001 | 129 | -1 | -126 | -127 |
| … | … | … | … | … |
| 1111, 1110 | 254 | -126 | -1 | -2 |
| 1111, 1111 | 255 | -127 | -0(负零) | -1 |
理解原码和补码的定义不难,理解补码作用也不难,难的是理解补码是怎么设计出来的,总不可能是被树上的苹果砸到后想到的吧?
这就要提到数学中的 “补数” 概念:
听起来很抽象对吧❓其实生活中,就有一个更加形象的例子 —— 时钟,时钟里就蕴含着补数的概念! 。
比如说,现在时钟的时针刻度指向 6 点,我们想让它指向 3 点,应该怎么做:
可以看到,对于时钟来说 -3 和 +9 竟然是等价的! 这是因为时钟只能 12 个小时,当时间点数超过 12 时就会自动丢失,所以 15 点和 3 点在时钟看来是都是 3 点。如果我们要在时钟上进行 6 - 3 减法运算,我们可以将 -3 等价替换为它的正补数 +9 后参与计算,从而将减法运算替换为 6 + 9 加法运算,结果都是 3.

理解了补数的概念后,我们再多看一个十进制的例子:我们要计算十进制 354365 - 95937 = 的结果,怎么做呢?
具体来说,如果我们限制十进制数的位长最多只有 6 位,那么模就是 1000000, -95937 对应的正补数就是 1000000 - 95937 = 904063 。此时,我们可以直接用正补数代替负数参与计算,则有:
354365 - 95937 // = 258428
= 354365 - (1000000 - 904063)
= 354365 - 1000000 + 904063 【减整加补】
= 258428
可以看到,把 -95937 等价替换为 +904063 后,就把减法运算替换为加法运算。细心的你可能要举手提问了,还是需要减去 1000000 呀?🙋🏻♀️ 。
其实并不用,因为 1000000 是超过位数限制的,所以减去 1000000 这一步就像时针逆时针拨动一整圈一样是无效的。所以实际上需要计算的是:
// 实际需要计算的是:
354365 + 904063
= 1258428 = 258428
^
最高位 1 超出位数限制,直接丢弃
继续使用前文提到的 14 + (-1) 正负数相加的例子:
// 原码表示法
0000, 1110 + 1000, 0001 = 1001, 1111 // 14 + (-1) = -15 错误
^ ^ ^
符号位 符号位 符号位
// 补码表示法
0000, 1110 + 1111, 1111 = 1, 0000, 1101 // 14 + (-1) = 13 正确
^ ^ ^
符号位 符号位 最高位 1 超出位数限制,直接丢弃
如果我们限制二进制数字的位长最多只有 8 位,那么模就是 1, 0000, 0000 ,此时, -1 的二进制数 1000, 0001 的正补数就是 1111, 1111 .
我们使用正补数 1111, 1111 代替负数 1000, 0001 参与运算,加法运算后的结果是 1, 0000, 1101 。其中最高位 1 超出位数限制,直接丢弃,所以最终结果是 0000, 1101 ,也就是 13,计算正确.
补码示意图 。
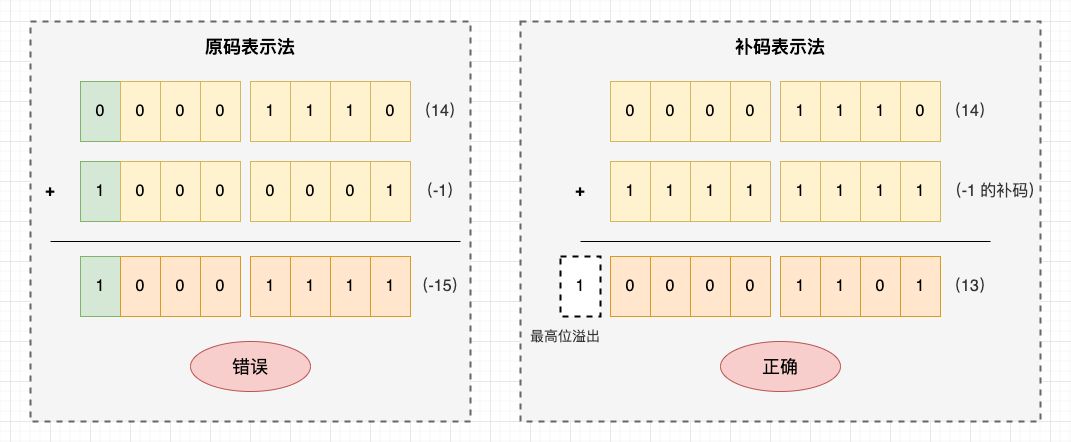
到这里,相信补码的设计原理已经很清楚了.
补码的关键在于: 找到一个与负数等价的正补数,使用该正补数代替负数,从而将减法运算替换为两个正数加法运算。 补码的出现与运算器的电路设计有关,从设计者的角度看,希望尽可能简化电路设计和计算复杂度。而使用正补数代替负数就可以消除减法器,实现简化电路的目的.
所以,小彭认为只有负数才存在补码,正数本身就是正数,根本就没必要使用补数,更不需要转为补码。而且正数使用补码的话,还不能把负数转补码的算法用在正数上,还得强行加一条 “正数的补码是原码本身” 的规则,就离谱好吧.
1、无符号数的编码中的每一位都可以用来存放数值信息,而有符号数需要在最高位留出一位符号位; 。
2、在有符号数的机器数运算中,需要对正数和负数采用不同的计算方法,而且需要引入减法器; 。
3、为了解决有符号机器数运算效率问题,计算机科学家们提出多种机器数的表示法:原码、反码、补码和移码; 。
4、使用补码表示法后,运算器可以消除减法运算,而且实现了 “0” 的机器数的唯一性; 。
5、补码的关键是找到一个与负数等价的正补数,使用该正补数代替负数参与计算,从而将减法运算替换为加法运算.
在前文讲补码的地方,我们提到计算机所有 “整型类型” 的负数都会使用补码表示法,刻意强调 “整数类型” 是什么原因呢,难道浮点数和整数在计算机中的表示方法不同吗?这个问题我们在 下一篇文章 里讨论,请关注.

最后此篇关于为什么计算机中的负数要用补码表示?的文章就讲到这里了,如果你想了解更多关于为什么计算机中的负数要用补码表示?的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
赏金:对于提供代码以使此子程序与负数一起工作的任何人,+50 信誉点。 我编写了一个 MIPS 程序来将华氏温度转换为摄氏温度。它打开自己的输出窗口(即 UART)并正确显示摄氏值。它在从 C 调用到
我得到了以下代码 # On va convertir en somme monétaire # We convert our integer into a way to read money
我得到了以下代码 # On va convertir en somme monétaire # We convert our integer into a way to read money
我使用以下 RegEx 基本上过滤掉任何文本,并接受数字 + 运算符。 ([-+]?[0-9]*\.?[0-9]+[\/\+\-\*])+([-+]?[0-9]*\.?[0-9]+) 所以它抓取 1+
我有一个查询,它计算我在查询中使用 union all 的平均值,以便获取我最终使用 max 函数的数据。 当联合返回结果时,如下所示:- col 1 col2 1 0
我有这样一个类: public class SpiralGenerator implements Iterator> { private void generate(int pos, E...
A = numpy.matrix([[36, 34, 26], [18, 44, 1], [11, 31, 41]]) X1 = numpy.matrix([[462
我有一个应用程序,其中有一个显示硬币 00 的 TextView ,一个按钮显示奖励视频广告,为用户提供 10 个硬币,还有一个购买按钮,将硬币减少 30 个。现在,当用户有 30 个硬币时,单击购买
话不多少,直接附上代码实例,仅供参考 ? 1
我有一系列正数和负数,我想将每个数字的绝对值增加一个,同时仍保持正数/负数。0.2 -> 1.2-0.3 -> -1.3我怎样才能做到这一点? 最佳答案 让我们尝试使用numpysign s=pd.S
我有这段代码,只允许在 keypress() 的输入字段中输入数字 if (e.which != 8 && e.which != 0 && (e.which 57)) { return fa
我试图用“-1”作为所有值填充二维数组。我正在使用的代码是: int c [] []=new int[4][4]; Arrays.fill(c,-1) 这会引发以下错误: Exception in t
在学校作业中,我们应该编写一个程序,该程序接受一个数字并将其分为三个部分:1. 检查数字是正数还是负数2. 整数(大小)3.小数部分 要求是应该有一个自己的函数,名为separate,具有输入和输出参
有没有什么方法可以在 C# 中执行整数除法(没有 float 或小数,我需要保持这个非常快)来向下舍入数字? 默认除法只是丢弃分数参数。考虑: 1 / 2 = 0 // That is correc
我正在使用 matplotlib 为报告生成图表,并指定我自己的样式表来指定文本格式以符合报告的指定文档样式。在我的 .mplstyle 样式表中,我按如下方式指定字体系列: font.family
在 C++11 中,如果我们尝试使用全局运算符 new 分配负大小的数组,它会抛出 std::bad_array_new_length,但是 C++98/C++03 呢?是 UB 还是会抛出 std:
我试过 scanf("%u",&number) 并且我输入了负数问题是当我 printf("%d",number) 我得到负数。我认为这会阻止我读取负数。scanf("%d",&number) 和 s
我的任务是解释一些看似奇怪的C代码行为(在x86上运行)。我可以轻松完成所有其他工作,但是这确实让我感到困惑。 代码段1输出-2147483648 int a = 0x80000000; int
js有问题吗? if("hello".indexOf("world")) { // I forgot to add > -1 here console.log("hello world");
我正在尝试使用 Antlr 4 设置一个简单的计算器。 语法: grammar calcGrammar; input : expression EOF; expression : MINUS

我是一名优秀的程序员,十分优秀!