本文已收录到 AndroidFamily ，技术和职场问题，请关注公众号 [彭旭锐] 提问.

前言

大家好，我是小彭.

在前几篇文章里 ，我们聊到了 Java 中的几种线性表结构，包括 ArrayList、LinkedList、ArrayDeque 等。今天，我们来讨论另一种常用的基础数据结构，同时也是 “面试八股文” 的标准题库之一 —— 散列表（Hash Table）.

同时，在后续的文章里，我们将以 Java 语言为例，分析标准库中实现的散列表实现，包括 HashMap 、ThreadLocalMap、 LinkedHashMap 和 ConcurrentHashMap。请关注.

---

小彭的 Android 交流群 02 群已经建立啦，扫描文末二维码进入~ 。

---

思维导图:

---

1. 什么是散列表？

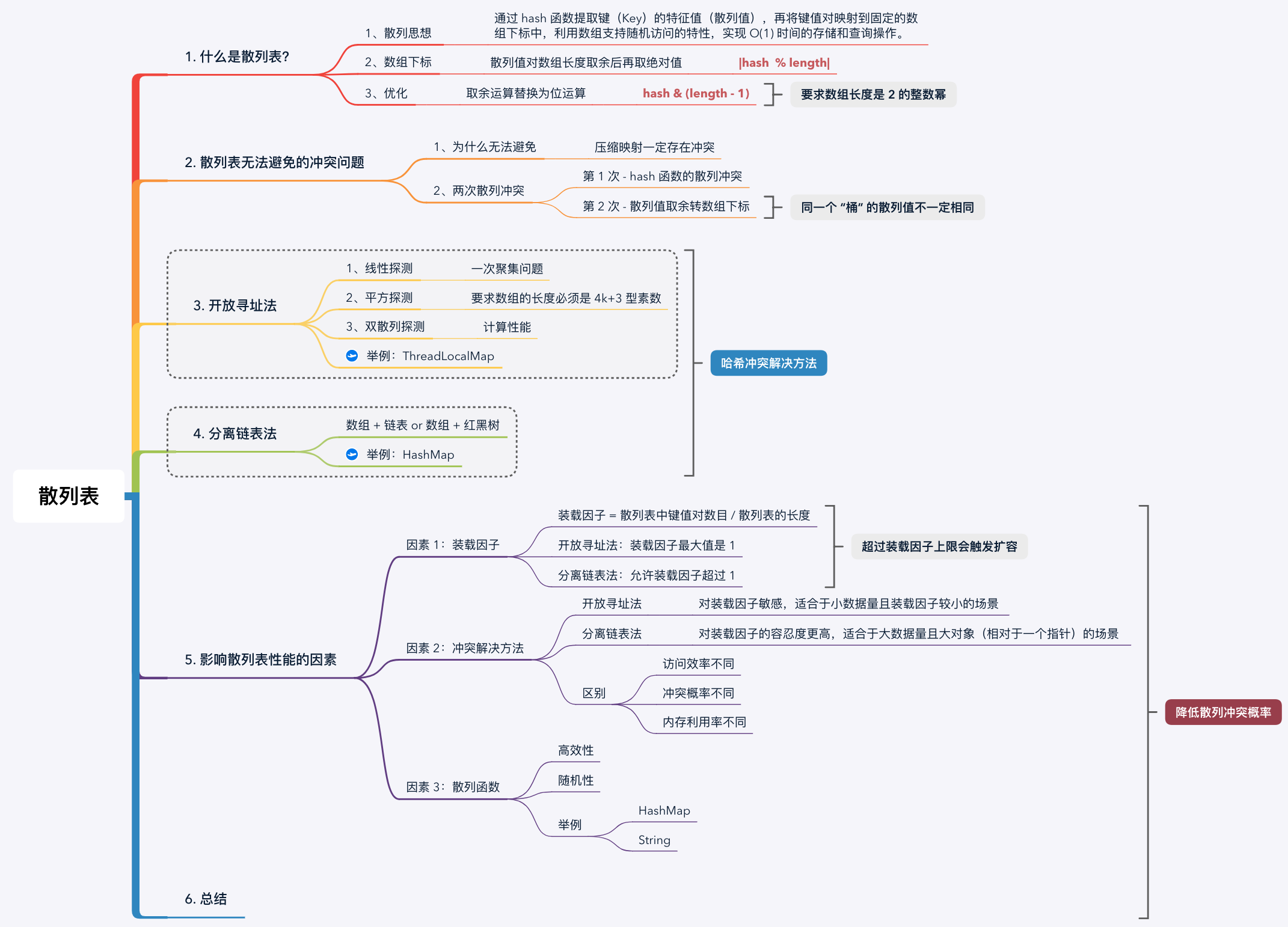
散列表是基于散列思想实现的 Map 数据结构，散列思想是散列表的核心特性，也就做哈希算法或 Hash 算法。散列算法是一种将 “任意长度的输入数据” 映射为 “固定长度的特征值” 的算法，输出的特征值就是散列值.

用一个表格总结散列算法的主要性质:

性质	描述
1、单向性（基本性质）	支持从输入生成散列值，不支持从散列值反推输入
2、高效性（基本性质）	单次散列运算计算量低
3、一致性（基本性质）	相同输入重复计算，总是得到相同散列值
4、随机性（高效性质）	散列值在输出值域的分布尽量随机
5、输入敏感性（高效性质）	相似的数据，计算后的散列值差别很大

将散列思想应用到散列表数据结构上时，就是通过 hash 函数提取键（Key）的特征值（散列值），再将键值对映射到固定的数组下标中，利用数组支持随机访问的特性，实现 O(1) 时间的存储和查询操作.

事实上，一般不会直接使用 hash 函数计算后的散列值作为数组下标。例如 Java Object#hashCode() 散列值是 int 类型，值域足足有 2^32 的容量，我们不可能创建这么大的数组.

最简单的做法是将散列值对数组长度取余后再取绝对值： |hash % length| 。如果数组长度 length 是 2 的整数幂，还可以等价替换成位运算： hash & (length - 1) ，不管被除数是正负结果都是正数。 不仅将取余运算替换为位运算，而且减少了一次取绝对值运算，提高了索引的计算效率.

                        
                          10  % 4 = 2
-10 % 4 = -2      // 负数
10  & (4 - 1) = 2
-10 & (4 - 1) = 2 // 正数

                        
                      

散列表示意图 。

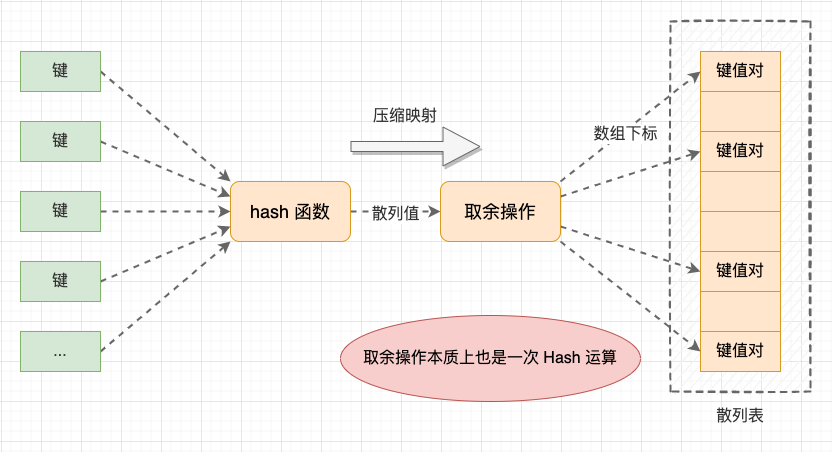
提示： 虽然我们将取余运算优化为位运算，但是为了便于理解，我们在后文中依然描述为逻辑上的 “取余” 运算.

---

2. 散列表无法避免的冲突问题

因为 Hash 算法会将非常大甚至无穷大的输入值域映射到 “固定长度的特征值”，所以 Hash 算法一定是压缩映射。例如，MD5 的输出散列值为 128 位，SHA256 的输出散列值为 256 位，这就存在 2 个不同的输入产生相同输出的可能性。这就是散列冲突或哈希冲突（Hash Collision）问题.

事实上，在散列表的设计中存在 2 次散列冲突:

• 第 1 次 - hash 函数的散列冲突： 这是一般意义上的散列冲突； 。

• 第 2 次 - 散列值取余转数组下标： 本质上，将散列值转数组下标也是一次 Hash 算法，也会存在散列冲突。同时，这也说明 HashMap 中同一个桶中节点的散列值不一定是相同的.

其实，散列冲突只要用鸽巢原理（又称：抽屉原理）就很好理解了，假设有 10 个鸽巢，现有 11 只鸽子，无论分配多么平均，也肯定有一个鸽巢里有两只甚至多只鸽子。举一个直接的例子，Java 中的字符串 "Aa" 与 "BB" 的就存在散列冲突.

散列冲突举例 。

                        
                          String str1 = "Aa";
String str2 = "BB";
System.out.println(str1.hashCode());  // 2112
System.out.println(str2.hashCode());  // 2112 散列冲突

                        
                      

由于我们无法避免散列冲突，所以只能保证散列表不会因为散列冲突而失去正确性。常用的散列冲突解决方法有 2 类:

• 开放寻址法： 例如 ThreadLocalMap；
• 分离链表法： 例如 HashMap。

---

3. 开放寻址法

开放寻址（Open Addressing）的核心思想是： 在出现散列冲突时，在数组上重新探测出一个空闲位置。 经典的探测方法有线性探测（Linear Probing）、平方探测（Quadratic Probing）和双散列探测（Double Hashing Probing）.

3.1 线性探测

线性探测是最基本的探测方法，在 Java 实现线程局部存储的 ThreadLocal 类中的散列表，就是基于线性探测的散列表。ThreadLocal 我们会在后续专栏文章会讨论，请关注.

• 添加键值对： 先将散列值取余映射到数组下标，然后从数组下标位置开始探测与目标 Key 相等的节点。如果找到，则将旧 Value 替换为新 Value，否则沿着数组顺序线性探测。直到线性探测遇到空闲位置，则说明节点不存在，需要添加新节点。如果在添加键值对后数组没有空闲位置，就触发扩容； 。

• 查找键值对： 查找类似。也是先将散列值映射到数组下标，然后从数组下标位置开始线性探测。直到线性探测遇到空闲位置，则说明节点不存在； 。

• 删除键值对： 删除类似。由于查找操作在遇到空闲位置时，会认为键值对不存在于散列表中，如果删除操作时 “真删除”，就会使得一组连续段产生断层，导致查找操作失效。因此，删除操作要做 “假删除”，删除操作只是将节点标记为 “Deleted”，查找操作在遇到 “Deleted” 标记的节点时会继续向下探测.

开放寻址法示意图 。

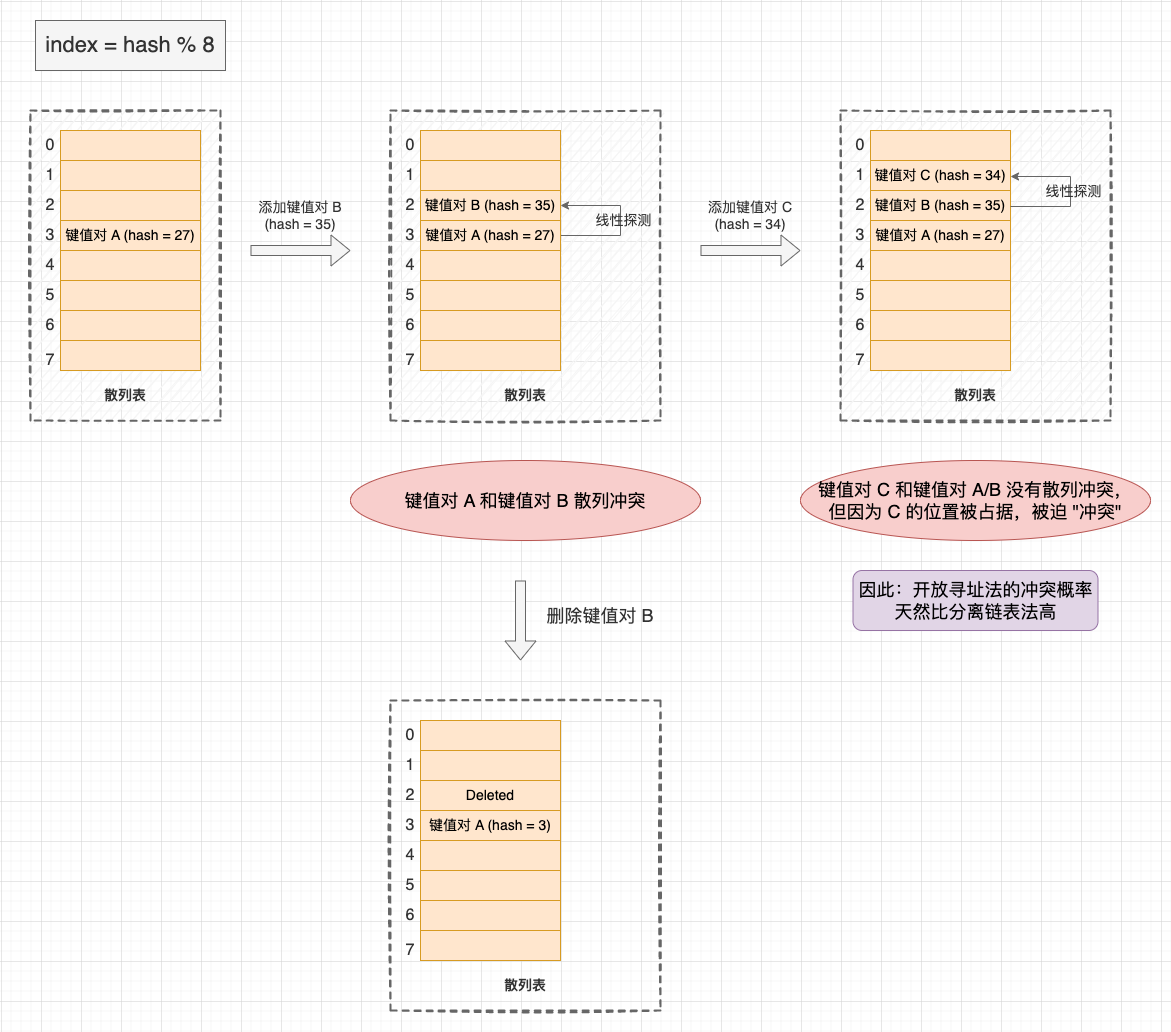
线性探测的缺点是 “一次聚集” 问题： 不仅会让散列冲突的键值对聚集，还会让原本没有散列冲突但位置被占用的节点被迫聚集在一起，降低了添加和查找效率。最坏情况下，有可能需要线性探测整张散列表才能找到目标位置.

3.2 平方探测法

平方探测与线性探测类似，区别在于： 线性探测的探测指针是一个线性序列，而平方探测的探测指针是一个平方序列。使用平方探测并不能完全解决 “聚集” 问题，但相比于线性探测聚集现象有所减弱.

需要特别注意， 平方探测法必须要求数组的长度必须是 4k+3 型素数， 才能保证能够探测完整个数组空间，否则会出现数组有空闲位置，但平方探测找不到的情况，此时扩容显得没有必要.

3.3 双散列探测

双散列探测的核心思想是： 提供一组散列函数，在遇到计算得到的数组下标位置被占用，则使用下一个散列函数重新计算，直到找到空闲位置.

对比下 3 种方法的探测步骤:

• 线性探测： hash(key) + 0，hash(key) + 1，hash(key) + 2，hash(key) + 3… 。

• 平方探测： hash(key) + 0^2，hash(key) + 1^2，hash(key) + 2^2，hash(key) + 3^2… 。

• 双散列探测： hash(key)，hash1(key)，hash2(key)，hash3(key)… 。

---

4. 分离链表法

分离链表法（Separate Chaining）的核心思想是： 在出现散列冲突时，将冲突的元素添加到同一个桶（Bucket / Slot）中，桶中的元素会组成一个链表，或者跳表、红黑树等动态数据结构.

相较之下，链表法是更常用且更稳定的冲突解决方法，我们熟悉的 Java HashMap 就是基于分离链表法的实现。HashMap 我们会在后续专栏文章会讨论，请关注.

• 添加键值对： 先通过散列函数将散列值映射到数组下标，然后沿着链表寻找节点的 Key 和添加的 key 相等的节点。如果找到，则将旧 Value 替换为新 Value，如果找不到，则创建在链表上新建节点； 。

• 查找键值对： 查找与添加的步骤类似，也是先将散列值映射到数组下标，然后沿着链表寻找节点的 Key 和添加的 key 相等的节点。如果找不到，则说明键值对不存在于散列表中； 。

• 删除键值对： 删除键值对不需要 “假删除”，与添加和查找类似，也是先将散列值映射到数组下标，然后沿着链表寻找节点的 Key 和添加的 key 相等的节点。如果找到，则将节点从链表上移除.

分离链表法示意图 。

---

5. 影响散列表性能的因素

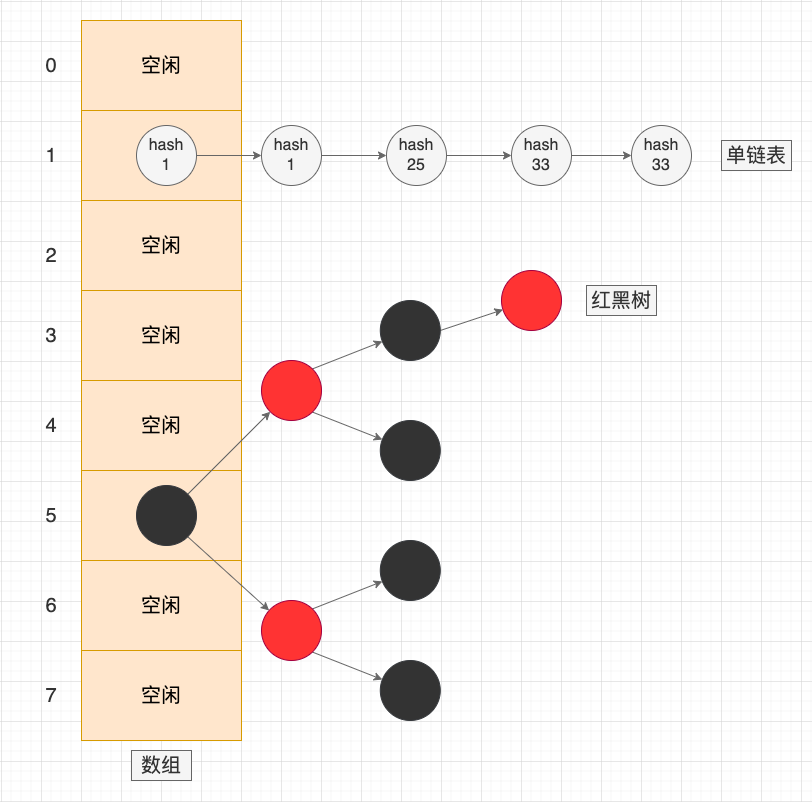
从上面的内容我们逐渐明白， 散列表操作的时间复杂度并不是绝对的 O(1)。 它与地址堆积的个数 K 或链表的长度 K 有关，也就是 O(K)。虽然 O(K) 也是常数时间复杂度，但并不是固定的常数。在极端情况下，当所有的数据都堆积在一起，或者所有数据都映射到相同的链表中时，时间复杂度就会从 O(1) 退化到 O(n).

换句话说，影响散列表性能的关键在于 “散列冲突的发生概率”，冲突概率越低，时间复杂度越接近于 O(1)。 那么，哪些因素会影响冲突概率呢？主要有 3 个：装载因子、冲突解决方法、散列函数.

5.1 因素 1 - 装载因子和扩容

理解了开放地址法和分离链表法两种冲突解决方法后，我们会发现： 无论使用哪种方法，随着散列表中元素越来越多，空闲位置越来越少，就会导致散列冲突的发生概率越来越大，使得散列表操作的平均时间会越来越大。为了描述散列表的装满程度，我们定义 装载因子 (Load Factor) = 散列表中键值对数目 / 散列表的长度.

• 在基于开放寻址法的散列表中： 装载因子的最大值是 1（数组装满），装载因子为 1 时无法添加新元素，必须扩容； 。

• 在基于分离链表法的散列表中： 允许装载因子超过 1（拉长出很长的链表），装载因子为 1 时，扩容并不是必须的.

                        
                          装载因子 = 散列表中键值对数目 / 散列表的长度

                        
                      

扩容本质上是扩大了散列算法的输出值域，扩大输出值域可以直接降低冲突概率。事实上，一般不会等到装载因子接近 1 时再扩容，而是设置一个处于 (0, 1) 之间的 装载因子上限（扩容阈值）。 例如，在 HashMap 中设置的默认装载因子上限是 0.75.

当散列表的装载因子大于扩容阈值时，就会触发扩容操作，并将原有的数据搬运到新的数组上。与普通数组相比，散列表的动态扩容不再是简单的数据搬运，因为数组的长度变化了，公式 hash & (length - 1) 的计算的下标位置也变了，所以这一扩容过程也叫 “再散列”（不要和双散列探测混淆）.

散列表的扩容过程 。

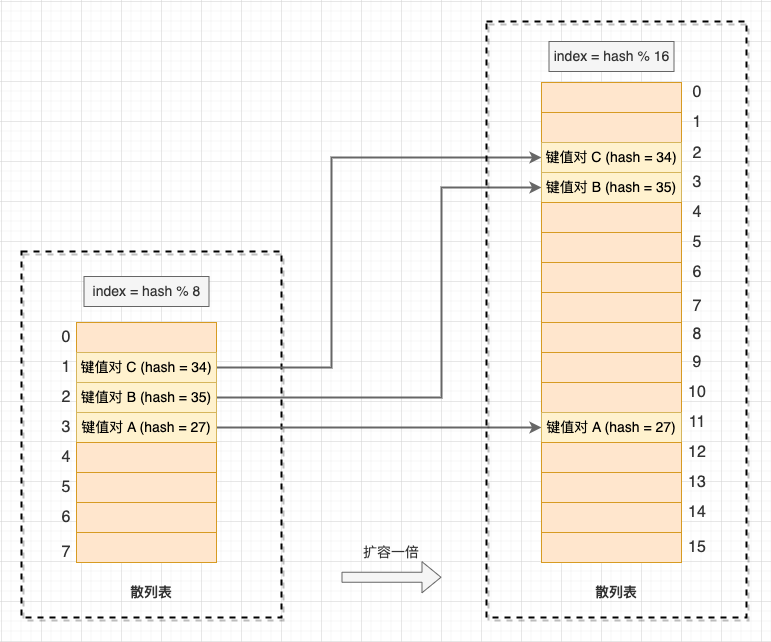
当添加操作触发扩容时，需要花费 O(n) 时间再散列和搬运数据，那么散列表的时间复杂度还是 O(1) 常数时间吗？对于这种大部分操作时间复杂度很低，只有个别情况下时间复杂度会退化，而且这些操作之间存在很强烈的顺序关系的情况，就很适合用 “均摊时间复杂度分析” 了。我们将花费 O(n) 时间的那一次插入操作的时间均摊到随后的多次 O(1) 时间插入操作上，那我们从整体看，添加数据的均摊时间复杂度就是 O(1).

以上是从算法分析的角度，从工程分析的角度看，事情还没这么简单。 在大数据场景下，如果旧散列表中有 1 GB 数据，那么扩容操作就是对 1 GB 的数据量做再散列。无论算法分析把时间复杂度摊还到多低，对 1 GB 数据量的再散列就是实打实的耗时操作，也是无法忍受的。此时，为避免一次性扩容过多数据的情况，有一种 “懒扩容” 方案：在创新一个新散列表的同时，保留旧的散列表。每次插入新的数据都插入到新散列表中，并从旧散列表中取一个数据再散列到新的散列表中。经过多次操作后，旧散列表中的数据就逐渐搬运到新散列表中.

5.2 因素 2 - 采用的冲突解决方法

开放寻址法和分离链表法的优缺点和适用场景不同:

• 1、访问效率不同： 开放寻址法中数据都存储在数组中，是一个连续的内存区域，基于局部性原理，开放寻址法能够更好地命中 CPU 缓存行。而分离链表法中的数据主要位于链表中，是离散的内存区域，对 CPU 缓存行不优友好； 。

• 2、冲突概率不同： 开放寻址法的冲突概率天然比分离链表法高，这是因为开放寻址法在发生冲突后，会在临近的位置寻找空闲位置填充数据，这使得原本并没有 “冲突” 的键值对也会因为没有空闲位置而被迫堆积。而分离链表法只有确实发生冲突的键值对才会堆积到同一个桶中； 。

• 3、内存利用率不同： 由于开放寻址法的冲突概率更高，所以装载因子上限不能设置很高，存储相同的数据量，开放寻址法也需要预先申请更大的数组空间，内存利用率不会高。当然，分离链表法在链表指针上也有额外内存消耗，如果存储的元素的内存量远远大于一个指针的内存量，则可以忽略不及.

综上所述，它们各自的适用场景是什么呢?

• 开放寻址法 - 对装载因子敏感，适合于小数据量且装载因子较小的场景： 例如 Java 的 ThreadlLocalMap，因为项目中不会大量使用 ThreadLocal 线程局部存储，所以它是一个小规模数据场景，这里使用开发地址法是没问题的； 。

• 分离链表法 - 对装载因子的容忍度更高，适合于大数据量且大对象（相对于一个指针）的场景： 例如，Java 中更通用的 HashMap 散列表就是采用分离链表法。而且，分离链表法还能够使用更多灵活的优化策略，例如将链表树化为红黑树，避免极端情况下时间复杂度退化为 O(n).

5.3 因素 3 - 散列函数设计

散列算法随机性和高效性也会影响散列表的性能。如果散列值不够随机，即使散列表整体的装载因子不高，也会使得数据聚集在某一个区域或桶内，依然会影响散列表的性能。如果散列算法不够高效，也会直接消耗计算性能.

---

6. 总结

• 1、散列表是基于散列思想实现的 Map 数据结构，就是通过 hash 函数提取键（Key）的特征值（散列值），再将键值对映射到固定的数组下标中，利用数组支持随机访问的特性，实现 O(1) 时间的存储和查询操作； 。

• 2、当数组的长度为 2 的整数幂时，可以将取余运算转换为位运算 hash & (length - 1) ，提高索引的计算效率； 。

• 3、由于散列值算法是压缩映射，所以散列表永远无法避免散列冲突，常用的散列冲突解决方法有开放寻址法和分离链表法； 。

• 4、开放寻址（Open Addressing）的核心思想是在出现散列冲突时，在数组上重新探测出一个空闲位置。 经典的探测方法有线性探测、平方探测和双散列探测； 。

• 5、分离链表法（Separate Chaining）的核心思想是在出现散列冲突时，将冲突的元素添加到同一个桶（Bucket / Slot）中，桶中的元素会组成一个链表，或者跳表、红黑树等动态数据结构； 。

• 6、开放寻址法对装载因子敏感，适合于小数据量且装载因子较小的场景。分离链表法对装载因子的容忍度更高，适合于大数据量且大对象（相对于一个指针）的场景； 。

• 7、采用的散列冲突解决方法、装载因子和散列函数设计都会影响散列表性能.

今天，我们聊了散列表的整体设计思想。在后续几篇文章里，我们将讨论散列表的具体实现 —— HashMap 。请关注.

---

参考资料

• 数据结构与算法分析 · Java 语言描述（第 5 章 · 散列）—— [美] Mark Allen Weiss 著
• 算法导论（第 11 章 · 散列表）—— [美] Thomas H. Cormen 等 著
• 散列算法 —— 维基百科
• 数据结构与算法之美（第 18~22 讲） —— 王争 著，极客时间 出品

最后此篇关于如何实现一个优秀的HashTable散列表？的文章就讲到这里了,如果你想了解更多关于如何实现一个优秀的HashTable散列表？的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。