First——什么是三门问题

三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）.

​ —— 百度百科 。

三门问题，很形象，就是你面前有三扇门.

其中有一扇门后面有一辆汽车，其余的两扇门后面是羊（咩~~）.

你随便选了一扇门，如果你很幸运地选到了车，你就能把它开走！ 。

但就在你将要打开门，看看后面是什么东西的时候， 。

好心的主持人 Monty Hall 打开了另外两扇门中后面有羊的一扇.

那么，你现在是否要把选的换成另一扇未开启的门呢.

。。。叙述可能有点不清楚 。。。

Second——反直觉

按理来说，你应该相信直觉，坚定地推开原来选的那扇门~~~~ 。

但实事实证明，如果你不相信自己的直觉（换成另外一扇门），那么你赢得车的概率要大很多.

是不是很反直觉.

明显是换不换都一样啊！ 。

于是，很多人都开始争论这个问题.

甚至把 IQ 最高的人类 玛丽莲·沃斯·莎凡特（Marilyn vos Savant） 也拉了过来讨论.

她却认为必须换，因为换了得到汽车的概率是 ​   .

为什么呢？她是这么想的:

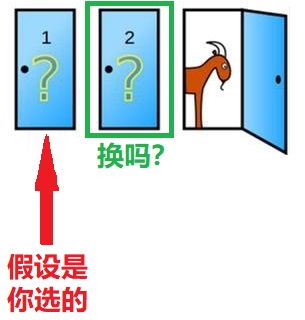
首先，你随便选了一扇门，那么剩下两扇门后是车的概率为 ​   ​ .

然后好心的主持人帮你在剩下两扇门中排除了一扇.

于是，神奇的结果出现了——剩下的最后一扇门后是车的概率就变成了 ​   ！！！ 。

这么一说，好像也对哈.

但还是很反直觉啊！！！ 。

所以，这个 IQ 最高的人，被一群人发送抱怨信，质疑她的说法.

我也有点晕，但也不会给她写抱怨信.

那么，就让事实来证明谁对谁错吧！ 。

Third——暴力枚举100万次

暴力枚举，这种事情当然交给计算机来做啊~ 。

写个代码枚举它个100万次就行了.

Code 很简单啦~~

                        
                            #   include   <iostream>  
                            #   include   <cstring>  
                            #   include   <cstdio>  
                            #   include   <algorithm>  
                            #   include   <ctime>  
                            #   include   <cstdlib>  
                           using 
                           namespace 
                           std
                           ; 
                           int 
                           main 
                           ( 
                           ) 
                           { 
                           freopen 
                           ( 
                           "数据.txt" 
                           , 
                           "w" 
                           , 
                           stdout 
                           ) 
                           ; 
                           //把数据写入文件 
                           srand 
                           ( 
                           time 
                           ( 
                           0 
                           ) 
                           ) 
                           ; 
                           //随机种子初始化 
                           int 
                           res 
                           = 
                           0 
                           ; 
                           //记录换的话是车的次数 
                           for 
                           ( 
                           int 
                           h 
                           = 
                           1 
                           ; 
                           h 
                           <= 
                           1000000 
                           ; 
                           ++ 
                          h
                           ) 
                           { 
                           //枚举100万次 
                           bool 
                           a
                           [ 
                           3 
                           ] 
                           = 
                           { 
                           0 
                           } 
                           ; 
                           //a就存门后的东西，0代表羊，1代表车，用一个bool数组就可以，要初始化都为0 
                          
		a
                           [ 
                           rand 
                           ( 
                           ) 
                           % 
                           3 
                           ] 
                           = 
                           1 
                           ; 
                           //随机选一个为车 
                           int 
                           t 
                           = 
                           rand 
                           ( 
                           ) 
                           % 
                           3 
                           , 
                           l 
                           = 
                           rand 
                           ( 
                           ) 
                           % 
                           3 
                           ; 
                           //t是你选的，l是剩下中打开后面是羊的门 
                           while 
                           ( 
                          l 
                           == 
                           t
                           ) 
                           l 
                           = 
                           rand 
                           ( 
                           ) 
                           % 
                           3 
                           ; 
                           //保证是剩下的 
                           if 
                           ( 
                          a
                           [ 
                          l
                           ] 
                           ) 
                           l 
                           = 
                           3 
                           - 
                           l 
                           - 
                           t
                           ; 
                           //如果要打开的选成车了，就选另外一个 
                           int 
                           x 
                           = 
                           3 
                           - 
                           l 
                           - 
                           t
                           ; 
                           //确定要选的 
                           if 
                           ( 
                          a
                           [ 
                          x
                           ] 
                           ) 
                           ++ 
                          res
                           ; 
                           //如果是车，次数+1 
                           if 
                           ( 
                          h 
                           % 
                           50 
                           == 
                           0 
                           ) 
                           { 
                           //每枚举50次就输出一次比率 
                           printf 
                           ( 
                           "%.5lf\n" 
                           , 
                           ( 
                           double 
                           ) 
                          res 
                           / 
                           h
                           ) 
                           ; 
                           //保留5位小数 
                           } 
                           } 
                           return 
                           0 
                           ; 
                           } 
                        
                      

最后的结果如下:

可以看到最后的结果已经非常逼近 ​ 了，这也证明世界上 IQ 最高的人还是名不虚传啊！ 。

最后此篇关于三门问题暴力枚举~~~的文章就讲到这里了,如果你想了解更多关于三门问题暴力枚举~~~的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。